core

Fill in a module description here 
import numpy as np
from numpy import linalg as LA

Unit

q1 = Q(-75, 'ncoulomb')

Summary

Key ideas: - Electron energy levels are discrete - Ionization energy

The energy emits when electron make transition between energy levels

Rydberg
10973731.56816
lambdaa, nu = smp.symbols('lambda nu')
lambdaa
lambda
nu
nu
n_i, n_f = smp.symbols('n_i n_f')
n_i
n_i
formula = (Rydberg*h*c) * ((1/n_i**2) - (1/n_f**2))
formula
2.17987236110358e-18/n_i**2 - 2.17987236110358e-18/n_f**2
eq = smp.Eq(1/lambdaa, formula)
eq
Eq(1/lambda, 2.17987236110358e-18/n_i**2 - 2.17987236110358e-18/n_f**2)
formula.subs(1, 2).evalf()
2.17987236110358e-18/n_i**2 - 2.17987236110358e-18/n_f**2
# #| export
# def the_wavelength_emit_from_transition(n1: 'the initial energy level', n2: 'the final energy level'):
#     formula = (Rydberg*h*c) * ((1/n_i**2) - (1/n_f**2))
#     formula_evaled = formula.subs([(n_i, n1), (n_f, n2)]).evalf()
#     equation = smp.Eq(1/lambdaa, formula_evaled)
#     return smp.solve(equation, lambdaa)
#energy_emit_from_transition(2, 1)
# the_wavelength_emit_from_transition(2, 1)

The energy that a photon carries

h
6.62607015e-34
c
299792458.0

\[\mathrm{E}=h \nu\] \[E=\frac{h c}{\lambda}\]

source

calculate_energy

 calculate_energy (**kwargs)
h
6.62607015e-34
c
299792458.0
h*c
1.9864458571489286e-25
calculate_energy(wavelength=525)
3.783706394569388e-28
calculate_energy(wavelength=3.37e-7)
5.894498092430055e-19
def calculate_wavelength_from_energy(energy):
    return energy/h
def calculate_wavelength_from_wavelength(frequency):
    pass
calculate_energy(wavelength=2)
9.932229285744643e-26

Emission Spectrum

Use energy transitions to characterize materials

Bond

  • Shell: like to be total filled > totally empty > partial filled

Oxidation state of an atom tells

from mendeleev import Si, Fe, O, Al, Ca, Ti, F, Cr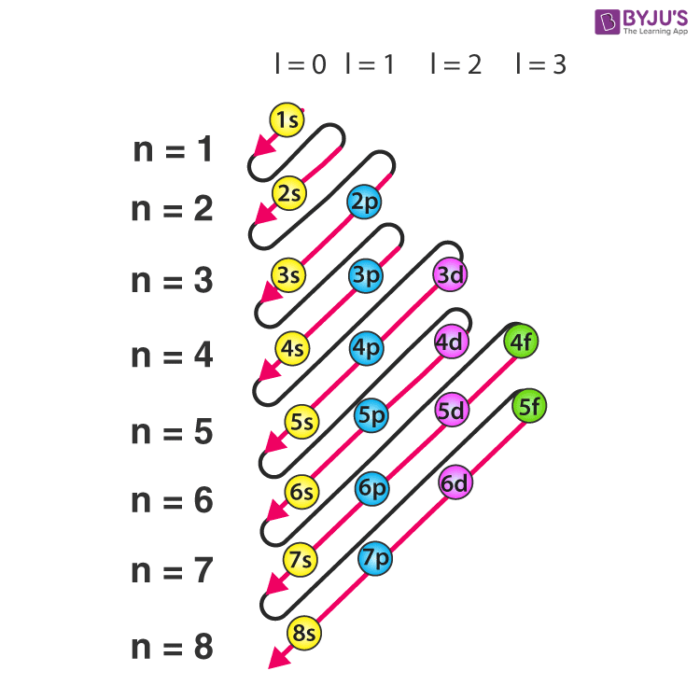

Si.name
'Silicon'
Al.oxistates
[3]
Ca.oxistates
[2]
Ti.oxistates
[4, 3, 2]
F.oxistates
[-1]
Cr.oxistates
[6, 3, 2]
Cr.ec.conf
OrderedDict([((1, 's'), 2),
             ((2, 's'), 2),
             ((2, 'p'), 6),
             ((3, 's'), 2),
             ((3, 'p'), 6),
             ((3, 'd'), 5),
             ((4, 's'), 1)])
Fe.ec.conf
OrderedDict([((1, 's'), 2),
             ((2, 's'), 2),
             ((2, 'p'), 6),
             ((3, 's'), 2),
             ((3, 'p'), 6),
             ((3, 'd'), 6),
             ((4, 's'), 2)])
Fe.oxistates
[3, 2]
from mendeleev import Na
Na.oxistates
[1]

Symbols